问题
问答题
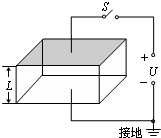
为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积A=0.04m2的金属板,间距L=0.05m,当连接到U=2500V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示.现把m=40mg的带有正电荷的烟尘颗粒密闭在容器内,假设这些颗粒的质量及所带电荷量均相同,在容器中均匀分布且都处于静止状态,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力,当合上开关S后经0.02s时间烟尘颗粒可以被全部吸附.请估算:
(1)每个烟尘颗粒的比荷(电荷量与质量之比)
(2)除尘过程中电场对烟尘颗粒共做了多少功?
答案
(1)当最靠近上表面的烟尘颗粒被吸附到下板时,烟尘就被全部吸附.烟尘颗粒受到的电场力F=
,qU L
L=
at2=1 2
,qUt2 2mL
解得
=q m
=5×10-3C/kg2L2 Ut2
(2)全部颗粒被吸附的过程可以等效为:全部颗粒从极板中间被吸附到负极板,所以加速电压为U 2
烟尘颗粒总的带电量q=5×10-3×4×10-5=2×10-7C
W=
=2.5×10-4J.qU 2
答:(1)每个烟尘颗粒的比荷为5×10-3C/kg.
(2)除尘过程中电场对烟尘颗粒共做了2.5×10-4J.
