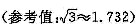问题
解答题
已知两个命题p:直线y=mx+3与圆(x-3)2+(y-2)2=4相交的弦长大于2
(1)当p为真时,求实数m的取值范围; (2)若p∨q为真,p∧q为假,求实数m的取值范围. |
答案
(1)当p为真时,圆心到直线的距离d=
,|3m+1| m2+1
所以弦长2
>24-d2
⇒4-d2>3⇒d2<1,即3
<19m2+6m+1 m2+1
整理得4m2+3m<0,即-
<m<0.3 4
∴当p为真时,实数m的取值范围是-
<m<0;3 4
(2)当q为真时,
⇒m<-3
+1+1 4
m-1<01 2 4+1+2m+1<0
若p∨q为真,p∧q为假,根据复合命题真值表知:命题p、q一真一假,
若p真q假时,
⇒--
<m<03 4 m≥-3
<m<0;3 4
若p假q真时,
⇒m<-3;m≥0或m≤- 3 4 m<-3
综上m的取值范围是-
<m<0或m<-3.3 4