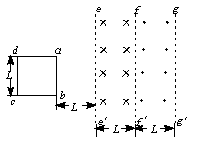
两个沿竖直方向的磁感强度大小相等、方向相反的匀强磁场穿过光滑的水平桌面，它们的宽度均为L.质量为m、边长为L的平放在桌面上的正方形线圈的ab边与磁场边界ee′的距离为L，如图所示.线圈在恒力作用下由静止开始沿桌面加速运动，ab边进入右边的磁场时恰好做速度为v的匀速直线运动.求：
（1）当ab边刚越过ff′时线圈的加速度.
(2)当ab边运动到ff′与gg′之间的正中间位置时，线圈又恰好做匀速直线运动，从ab边刚越过ee′到达右边磁场正中间位置的过程中，线圈 * * 生多少热量？
（1）a==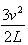
方向与运动方向相反.
(2) Q=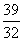
mv2
（1）设恒力为F，由线圈开始运动到ab边进入磁场前瞬间，根据动能定理
W=ΔEk得F=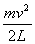
①
ab边刚越过ee′未到达ff′时做匀速运动，处于平衡状态，磁场力大小F1=F，设磁感强度为B，线圈电阻为R，则感应电动势E1=BLv
磁场力F1=BI1L
因为I1=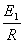
得F=
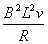②
当ab边刚越过ff′地，ab、cd边感应电动势大小、方向相同，总电动势ε2=2ε1,电流I2=2I1 ③
故磁场力的合力F2=4F1 ④
由牛顿第二定律和①、④式得
a=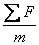
=
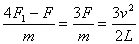
方向与运动方向相反.
(2)设ab边运动到ff′与gg′正中间时速度为v3,则感应电动势ε3=2BLv3，磁场力大小F3=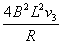
⑤
此时线圈又做匀速运动，磁场力的大小F3=F ⑥
由②、⑤、⑥式得v3=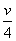
⑦
根据动能定理WF-WB=ΔEk
根据能量守恒定律，从ab边刚越过ee′到达右侧磁场正中间过程中，线圈产生的热量与磁场力做的功大小相等，得Q=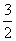
FL+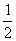
mv2-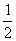mv23 ⑧
由①、⑦、⑧式得Q=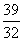mv2