(20分)如图所示，de和fg是两根足够长且固定在竖直方向上的光滑金属导轨，导轨间距离为L，电阻忽略不计。在导轨的上端接电动势为E，内阻为r的电源。一质量为m、电阻为R的导体棒ab水平放置于导轨下端e、g处，并与导轨始终接触良好。导体棒与金属导轨、电源、开关构成闭合回路，整个装置所处平面与水平匀强磁场垂直，磁场的磁感应强度为B，方向垂直于纸面向外。已知接通开关S后，导体棒ab由静止开始向上加速运动，求：
（1）导体棒ab刚开始向上运动时的加速度以及导体棒ab所能达到的最大速度；
（2）导体棒ab达到最大速度后电源的输出功率；
（3）分析导体棒ab达到最大速度后的一段时间△t内，整个回路中能量是怎样转化的？并证明能量守恒
（1）
（2）P
（3）电源的电能转化为导体棒的机械能和电路中产生的焦耳热之和。
（1）（10分）导体棒ab刚开始运动时的速度为零，由欧姆定律
（1分）
导体棒ab受安培力 
（1分）
牛顿第二定律 
（1分）
导体棒ab开始运动时的加速度 
（1分）
设导体棒ab向上运动的最大速度为
，当导体棒所受重力与安培力相等时，达到最大速度，回路电流为
（2分）
由欧姆定律 
（2分）
得 （2分）
（2）（4分）电源的输出功率 
（2分）
P （2分）
（3）（6分）电源的电能转化为导体棒的机械能和电路中产生的焦耳热之和（1分）
△t时间内：电源的电能 △E电=E△t
△t （1分）
导体棒ab增加的机械能
△E机= mg△t = mg
△t （1分）
电路中产生的焦耳热Q=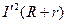
△t=
（R+r）△t （1分）
△t时间内，导体棒ab增加的机械能与电路中产生的焦耳热之和为△E’
△E’=△E机 + Q （1分）
△E’=mg△t + （R+r）△t
整理得 △E’△t （1分）
由此得到△E电=△ E’，回路中能量守恒