问题
问答题
如图所示,两足够长的直平行水平导轨相距 =1.0
=1.0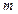 ,导轨左边连接阻值
,导轨左边连接阻值 =15
=15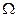 的电阻,导轨上放置着
的电阻,导轨上放置着 、
、 两金属捧,
两金属捧, 棒质量
棒质量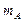 =0.75kg、电阻
=0.75kg、电阻 =10
=10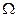 ,
, 棒质量
棒质量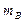 =0.25
=0.25 、电阻
、电阻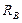 =10
=10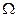 ,两金属棒与导轨垂直,两棒靠得很近,之间用长为
,两金属棒与导轨垂直,两棒靠得很近,之间用长为 =4.0m的绝缘轻绳相连,整个装置置于磁感应强度大小B=1.0T、方向竖直向下的匀强磁场中。从
=4.0m的绝缘轻绳相连,整个装置置于磁感应强度大小B=1.0T、方向竖直向下的匀强磁场中。从 =0开始对
=0开始对 棒施加水平向右的拉力
棒施加水平向右的拉力 ,使
,使 棒由静止开始以
棒由静止开始以 =2.0
=2.0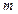 /s2的加速度做匀加速运动,
/s2的加速度做匀加速运动, =2.0s时撤去拉力
=2.0s时撤去拉力 。已知
。已知 棒右边的导轨是光滑的,轻绳绷紧前
棒右边的导轨是光滑的,轻绳绷紧前 棒静止不动,轻绳绷紧后,两棒以相同速度运动直至停止。导轨电阻不计。求:
棒静止不动,轻绳绷紧后,两棒以相同速度运动直至停止。导轨电阻不计。求:
(1)拉力 随时间
随时间 变化的关系式;
变化的关系式;
(2)轻绳绷紧后,电阻R上产生的焦耳热;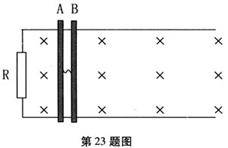
答案
(1)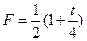 ,
,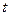 ≤2.0
≤2.0 (2)0.375J
(2)0.375J
(1)B棒运动时,其速度为:
感应电动势为:
电路总电阻为: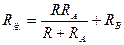
感应电流: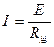
金属棒 受安培力为:
受安培力为: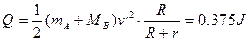
对金属棒,由牛顿定律得: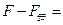 ma
ma
从而解得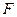 随
随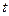 变化的关系式为:
变化的关系式为: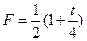 ,
,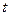 ≤2.0
≤2.0 (8分)
(8分)
(2)2.0s内B棒发生的位移为: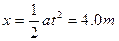 ,即撤去拉力
,即撤去拉力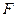 时绳恰好绷紧,
时绳恰好绷紧,
2.0s时,B棒的速度为:
绳绷紧时满足动量守恒: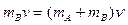
绳绷紧后,AB共同切割磁感线,其内阻
所以,电阻R上产生的热等为: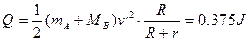 (10分)
(10分)
