问题
问答题
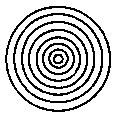
电磁炉专用平底锅的锅底和锅壁均由耐高温绝缘材料制成．起加热作用的是安在锅底的一系列半径不同的同心导电环(导电环的分布如图所示)．导电环所用材料每米的电阻为0.125πΩ，从中心向外第n个同心圆环的半径为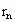
＝(2n－1)r，(n＝1，2，3，…，7)，已知
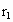＝1.0cm．当电磁炉开启后，能产生垂直于锅底方向的变化磁场，该磁场的磁感应强度B随时间的变化率为
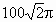sinωt，求：
(1)半径为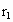的导电圆环中感应电流的最大值是多大？
(2)假设导电圆环产生的热全部以波长为1.0×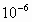
m的红外线光子辐射出来，那么半径为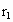的导电圆环上每分钟辐射出的光子数是多少？
(3)若不计其他损失，所有导电圆环释放的总功率P是多大？
(以上计算中可取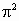
＝10，h＝6.6×
J·s．)
答案
（1）
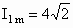A． （2）1.2×
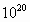(3) 1.9×
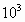W
(1)根据法拉第电磁感应定律E＝100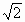
πSsinωt，第n环中的感应电动势最大值
，
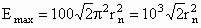第n环的电阻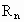
＝0.125π·2π
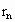＝2.5，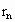
因此第n环中电流最大值为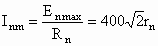
，
将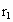
＝1.0cm＝
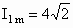m代入得A．
(2)根据能量守恒定律，设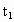
＝1min内辐射出的光子数为n，电能全部转化为光能
＝n·hc/λ，
其中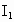
交变电流的有效值
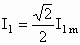＝4A，
代入数据计算得 n＝1.2×．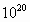
(3)P＝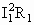
＝0.4W，
，
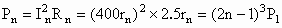共七个导电圆环，释放的总功率
P＝
＝1.9×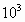W．