Travis laughed as he tore at the wrapping paper on his birthday present. He was so
! Finally, he would have the coolest pair of name-brand basketball shoes.
All the guys on his team were wearing the name-brand shoes of a popular basketball
, Chuck Hart.
Hart was criticized for his poor sportsmanship and infamous
, he was a great player. In fact, Travis wasn't thinking about Hart' s behavior; he had only expected to see Hart’s
on the side of the box. The first indication that something was
came as he tore away the last piece of paper. Not Hart’s. The new shoes were the name-brand of another player, Robert Ryann, who was
for his amazing work in the community.
Travis’s hands
; his heart stopped. It wasn't that the Ryann shoes weren’t nice, but what would his friends think ?
They were the wrong shoes and Travis would be
by the other players. When he looked up into his dad' s eyes, however, Travis decided he
not tell him. "'Thanks, Dad. I was really hoping for shoes," Travis said as he pulled the shoes out of the box.
Next morning his dad drove him to school. When they
in front of his destination, Travis slowly opened the car door. Just then, his dad stopped him.
“Hey, Travis, wait a minute, look…” his dad said
,“Travis, I know those aren’t the shoes you had hoped for, but I saw the names of the two guys and made a(n)
. The guy whose name is on those shoes,” he said, pointing down at Travis’s feet, “is someone I
. Do you know how often Ryann has found himself in
?”
“No,” Travis said.
“Never. He’s never talked back to his coach or started a fight, and he’s a team player. You could have acted like a (n)
when you didn’t get the shoes you wanted, Travis,
you were polite and made the best of it. You have such a good
, like the guy whose name is on these shoes. I’m hoping that someday, your name will be on the coolest pair of shoes I’ll ever see.”
When Travis looked down at his feet, he saw the shoes
. His dad had used his mind and heart to give the son a thoughtful
.
| 小题1: | | A.surprised | B.ashamed | C.excited | D.worried |
|
| 小题2: | | A.team | B.player | C.coach | D.game |
|
| 小题3: | | A.Unless | B.If | C.Because | D.Although |
|
| 小题4: | | A.skill | B.performance | C.behavior | D.action |
|
| 小题5: | | A.name | B.photo | C.sign | D.model |
|
| 小题6: | | A.strange | B.wrong | C.true | D.funny |
|
| 小题7: | | A.known | B.encouraged | C.adopted | D.influenced |
|
| 小题8: | | A.fell | B.froze | C.shook | D.folded |
|
| 小题9: | | A.questioned | B.noticed | C.teased | D.attacked |
|
| 小题11: | | A.pulled up | B.put up | C.took up | D.turned up |
|
| 小题12: | | A.peacefully | B.hesitantly | C.delightedly | D.naturally |
|
| 小题13: | | A.choice | B.effort | C.comment | D.mistake |
|
| 小题14: | | A.believe | B.miss | C.admire | D.remember |
|
| 小题15: | | A.danger | B.surprise | C.sorrow | D.trouble |
|
| 小题16: | | A.teammate | B.adult | C.kid | D.student |
|
| 小题18: | | A.quality | B.courage | C.dream | D.belief |
|
| 小题19: | | A.clearly | B.carefully | C.patiently | D.differently |
|
| 小题20: | | A.gift | B.look | C.hope | D.lesson |
|
 ,水平放置的平行金属导轨P、Q与金属板C、D接触良好,且导轨在磁感应强度为B1=10T的匀强磁场中,导轨间距L=0.50m.金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动.其速度图像如图(乙),若规定向右运动速度方向为正方向,从t=0时刻开始,由C板小孔O处连续不断飘入质量为m=3.2×10-21kg、电量q=1.6×10-19C的带正电的粒子(设飘入速度很小,可视为零).在D板外侧有以MN为边界的匀强磁场B2=10T,MN与D相距d=10cm,B1和B2方向如图(甲)所示(粒子重力及其相互作用不计),求:
,水平放置的平行金属导轨P、Q与金属板C、D接触良好,且导轨在磁感应强度为B1=10T的匀强磁场中,导轨间距L=0.50m.金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动.其速度图像如图(乙),若规定向右运动速度方向为正方向,从t=0时刻开始,由C板小孔O处连续不断飘入质量为m=3.2×10-21kg、电量q=1.6×10-19C的带正电的粒子(设飘入速度很小,可视为零).在D板外侧有以MN为边界的匀强磁场B2=10T,MN与D相距d=10cm,B1和B2方向如图(甲)所示(粒子重力及其相互作用不计),求: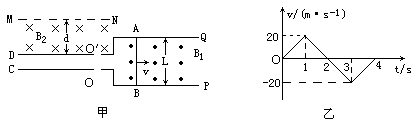
 ,而粒子要飞出磁场边界MN的最小速度v0必须满足
,而粒子要飞出磁场边界MN的最小速度v0必须满足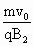 ,
, ,
, =20m/s时,产生感应电动势为
=20m/s时,产生感应电动势为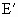 ,可得
,可得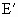 =B1L
=B1L =100V.
=100V.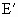 =
=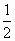 mv2,
mv2,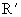 =
=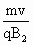 =0.2m.
=0.2m. 的水平距离为
的水平距离为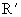 -
-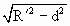 =0.027m=2.7cm.
=0.027m=2.7cm.
