问题
计算题
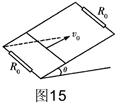
（16分）如图15所示，倾角为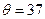
°、电阻不计、间距L=0.3m且足够长的平行金属导轨处在磁感应强度B=1T、方向垂直于导轨平面的匀强磁场中。导轨两端各接一个阻值Ro=2
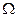的电阻。在平行导轨间跨接一金属棒，金属棒质量m=1kg，电阻r=2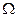,其与导轨间的动摩擦因数
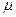=0.5。金属棒以平行于导轨向上的初速度
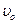=10m/s上滑直至上升到最高点的过程中，通过上端电阻的电荷量
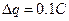(sin37°=0.6，cos37°=0.8,取g=10m/s2)求：
（1）金属棒的最大加速度
（2）上端电阻Ro中产生的热量
（3）金属棒上滑至最高点所用时间
答案
（1）
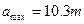/s2
（2）Q=5J
（3）Δt=0.994s
（1）金属棒在上滑的过程中，回路的总电阻为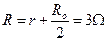
（1分）
对金属棒由牛顿第二定律得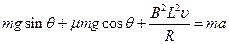 
（2分）
金属棒上滑过程中的最大加速度对应的是金属棒的最大速度，金属棒上升过程做减速运动，所以金属棒上升过程中的最大加速度就是速度为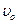
的瞬间,得：
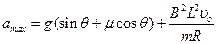（2分）
代入数据后得最大加速度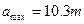/s2 （1分）
（2）由题设条件可知：金属棒上升到最高点的过程中通过金属棒中的电荷量为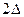
q，
设金属棒中的平均电流为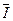
，则
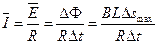（2分）
又通过金属棒的电荷量：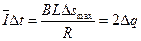
（*） （1分）；
设上端电阻产生的焦耳热为Q，则全电路产生的焦耳热为6Q，由能量守恒可知
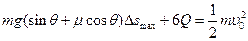（2分）；
联立以上各式，代入数据后 Q="5J " （1分）
（3）设金属棒上滑至最高点所用时间为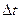
，则
由动量定理 
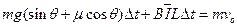（3分）；
联立（*）式，代入数据得 Δt="0.994s " （1分）