问题
计算题
如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为l ＝0.2m，在导轨的一端接有阻值为R ＝ 0.5Ω的电阻，在X ≥ 0处有一与水平面垂直的均匀磁场，磁感强度B ＝ 0.5T。一质量为m ＝ 0.1kg的金属直杆垂直放置在导轨上，并以v0＝2m/s的初速度进人磁场，在安培力和一垂直于杆的水平外力 F的共同作用下作匀变速直线运动，加速度大小为a ＝ 2m/s2，方向与初速度方向相反。设导轨和金属杆的电阻都可以忽略，且接触良好，求：
（1）电流为零时金属杆所处的位置；
（2）电流为最大值的一半时施加在金属杆上外力 F的大小和方向；
（3）保持其他条件不变，而初速度v0取不同值，求开始时F方向与初速度v0取值关系
答案
（1）感应电动势E＝ B l v， （1分）
感应电流 I=E/R （1分） I ＝ 0时，v ＝ 0 （1分）
此时，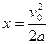
＝1（m） （2分）
（2）初始时刻，金属直杆切割磁感线速度最大，产生的感应电动势和感应电流最大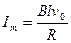 
（1分）
当感应电流为最大值的一半时，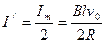
（1分）
安培力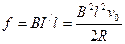
＝ 0.02 N （2分）
向右运动时：F ＋ f ＝ m a F ＝ m a － f ＝ 0.18 N，方向与x轴正方向相反（2分）
向左运动时：F － f ＝ m a F ＝ m a ＋ f ＝ 0.22 N，方向与x轴正方向相反（2分）
（3）开始时 v ＝ v0 ，
F ＋ f ＝ m a F ＝ m a － f ＝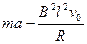
（4分）
∴当v0 ＜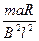 
＝ 10 m/s 时，F ＞0，方向与x轴正方向相反 （2分）
当v0 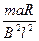＞ ＝ 10 m/s 时，F ＜0，方向与x轴正方向相同 （2分）