问题
计算题
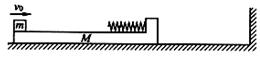
质量M=3kg的长木板静止在光滑水平面上，木板左侧放置一质量m=1kg的木块，右侧固定一轻弹簧，处于原长状态，弹簧正下方部分的木板上表面光滑，其他部分的木板上表面粗糙，如图所示现给木块v0=4m/s的初速度，使之向右运动，在木板与木块向右运动过程中，当木板和木块达到共速时，木板恰与墙壁相碰，碰撞过程时间极短，木板速度的方向改变，大小不变，最后木块恰好在木板的左端与木板相对静止。求：
①木板与墙壁相碰时的速度v1；
②整个过程中弹簧所具有的弹性势能的最大值Epm；
答案
①1m/s. ②3.75J
题目分析：①以木块与木板组成组成的系统为研究对象，从木块开始运动到两者速度相同的过程中，系统动量守恒，由动量守恒定律可得：mv0=（M+m）v1,解得：v1=1m/s.
②木板与墙壁碰后返回，木块压缩弹簧，当弹簧压缩到最短时，木块与木板速度相等，在此过程中两者组成的系统动量守恒，由动量守恒定律可得：Mv1-mv1=（M+m）v2,解得：v2=0.5m/s;
当弹簧压缩到最短时，弹性势能最大，由动能定理可得：
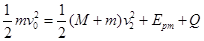
当木块到达木板最左端时两者速度相等，在此过程中，系统动量守恒，由动量守恒定律可得：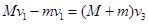
，解得v3=0.5m/s;
从木块开始运动到木块回到木板最左端的整个过程中，由能量守恒定律可知: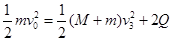 
，解得：Q=3.75J，EPm=3.75J.