问题
计算题
质量均为m的两个小物体A和B，静止放在足够长的水平面上，相距L=12.5m。它们跟水平面间的动摩擦因数均为μ=0.2，其中A带电荷量为q的正电荷，与水平面的接触是绝缘的，B不带电。现在水平面附近空间加一水平向右的匀强电场，场强
，A便开始向右运动，并与B发生多次对心碰撞，碰撞过程时间极短，每次碰撞后两物体交换速度，A带电量不变，B始终不带电。g取10 m/s2。试求：
（1）A与B第1次碰撞后B的速度大小；
（2）A与B从第5次碰撞到第6次碰撞过程中B运动的时间；
（3）B运动的总路程。
答案
解：（1）对A，根据牛顿第二定律：Eq－μmg=maA
解得加速度aA=1 m/s2
根据公式vA12=2aAL
解得A与B碰前速度vA1=5 m/s
碰撞交换速度，第1次碰后，A的速度为0，B的速度vB1=vA1=5 m/s
（2）对B，根据牛顿第二定律：μmg=maB
解得加速度大小aB=2 m/s2
每次碰后B做匀减速运动，因其加速度大于A的加速度，所以B先停，之后A追上再碰，每次碰后A的速度均为0，然后加速再与B发生下次碰撞
第1次碰撞：碰后B运动的时间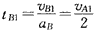
第2磁碰撞：碰前A的速度为vA2，则vA22=2aAxB1
XB1为第1磁碰后B的位移，则vB12=vA12=2aBxB1
由以上两式得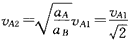
碰后B的速度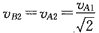
碰后B运动的时间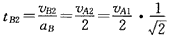
以此类推，第5次碰撞后B运动的时间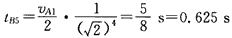
（3）解法1：经过无数次碰撞，最终A、B停在一起；每次碰撞交换速度，说明碰撞过程无机械能损失，设B运动的总路程为x，根据能量守恒Eq（L+x）=μmg（L+x）+μmgx
解得x=12.5m
解法2：根据第（2）问的分析，经过n次碰撞后B的速度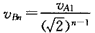
从第1次碰撞到第n次碰撞后B通过的总路程
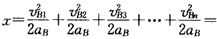
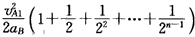
所以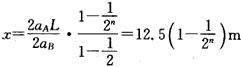
当n→∞时，即得B通过的总路程x=12.5m