给出定义：若m-12＜x≤m+12（其中m为整数），则m叫做离实数x最近

问题填空题

给出定义：若m-

＜x≤m+

（其中m为整数），则m叫做离实数x最近的整数，记作{x}=m．在此基础上给出下列关于函数f（x）=|x-{x}|的四个命题：
①函数y=f（x）的定义域为R，值域为[0，

]；
②函数y=f（x）的图象关于直线x=

（k∈Z）对称；
③函数y=f（x）是周期函数，最小正周期为1；
④函数y=f（x）在[-

，

]上是增函数．
其中正确的命题的序号______．

答案

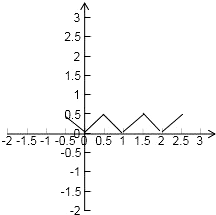
由题意x-{x}=x-m，f（x）=|x-{x}|=|x-m|，

m=0时，-

＜x≤

，f（x）=|x|，

m=1时，1-

＜x≤1+

，f（x）=|x-1|，

m=2时，2-

＜x≤2+

，f（x）=|x-2|，

由图象可知正确命题为①②③，

故答案为：①②③．