问题
解答题
如图所示,在△ABC中,AB>AC,AD是内角平分线,AM是BC边上的中线,求证:点M不在线段CD上.
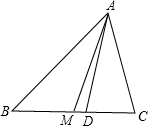
答案
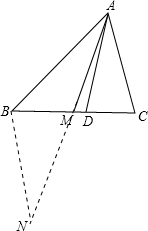
假设点M不在线段CD上不成立,则点M在线段CD上.
延长AM到N,使AM=MN,连接BN;
在△AMC和△NMB中,
BM=CM,∠AMC=∠BMN,AM=MN,
∴△AMC≌△NMB(SAS);
∴∠MAC=∠MNB,BN=AC;
根据M在线段CD上,则∠BAM>∠MAC,
∴∠MNB<∠BAM,
∴BN>AB,
即AC>AB;与AB>AC相矛盾.
因而M在线段CD上是错误的.
所以点M不在线段CD上.
