如图所示,水平地面上一个质量M="4.0" kg、长度L="2.0" m的木板,在F="8.0" N的水平拉力作用下,以v0="2.0" m/s的速度向右做匀速直线运动.某时刻将质量m="l.0" kg的物块(物块可视为质点)轻放在木板最右端。

(1)若物块与木板间无摩擦,求木板的加速度及物块离开木板所需的时间;
(2)若物块与木板间有摩擦,且物块与木板间的动摩擦因数和木板与地面间的动摩擦因数相等,求将物块放在木板上后,经过多长时间木板停止运动。(结果保留二位有效数字)
(1)0.50 m/s2;1.2 s.(2)4.0 s
题目分析:(1)未放物块之前,木板做匀速运动.因此木板与地面之间的动摩擦因数
μ =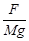 = 0.20
= 0.20

若物块与木板间无摩擦,物块放在木板上后将保持静止.木板水平方向受力如图1所示,它将做匀减速直线运动,设其加速度的大小为a1.
a1 = =" 0.50" m/s2
=" 0.50" m/s2
设物块经过时间t离开木板. 木板在这段时间内的位移 L = v0t- a1t2
a1t2
解得: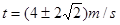 ,
,
即 t =" 1.2" s或6.8 s
(其中t =" 6.8" s不合题意舍去)
(2)若物块与木板间的动摩擦因数也为μ,则物块放在木板上后将做匀加速运动,设物块的加速度的大小为a2.
μmg = ma2
木板水平方向受力如图所示,它做匀减速直线运动,设其加速度的大小为a3.

μ (M+m) g + μmg-F = Ma3
设经时间tⅠ,物块与木板速度相等,此时它们的速度为v,此过程中木板的位移为s1,物块的位移为s2.
v = v0-a3tⅠ
v = a2tⅠ
s1 = v0tⅠ- a3tⅠ2
a3tⅠ2
s2 = a2tⅠ2
a2tⅠ2
可求a2 =μg =" 2.0" m/s2
a3 ="1.0" m/s2
v =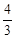 m/s,s1 =
m/s,s1 = m,s2 =
m,s2 =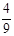 m
m
解得 tⅠ=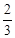 s,
s,
因为s1-s2< L,所以物块仍然在木板上.之后,它们在水平方向的受力如图所示,二者一起做匀减速直线运动,设它们共同运动的加速度的大小为a4.
μ (M+m) g-F =" (M+m)" a4

设再经过时间tⅡ,它们停止运动.
0 = v-a4tⅡ
tⅡ=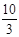 s
s
t总 = tⅠ+ tⅡ=" 4.0" s
因此将物块放在木板上后,经过 4.0 s木板停止运动.
