问题
填空题
△ABC中,AB=AC,∠BAC=120°,点D为AB中点,点E在BC上,CE=3BE,AE与CD交于点F,若AF=
|
答案
作AO⊥BC,连接DE,做AH∥CB交CD延长线于点H.
易证△ADH全等△BDC,∴AH=BC
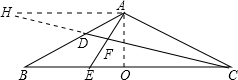
,
∵CE=3BE,
∴CE=
BC,CE=3 4
AH,3 4
∴EF:AF=CE:AH=3:4,
∴AF:AE=4:7,
∴AE=7 9
∴CF:HF=CE:AH=3:4 CF:CH=3:7,CH=2CD,CF:CD=6:7
∵BE:BO=BD:BA=1:2,
∴DE∥AO,
∵∠BAC=120°,
∴∠B=30°,
∴∠BDE=60°,
∵BD=2DE,
∴AD:DE=CA:AD=2,
∵∠ADE=∠CAD=120°
∴△ADE∽△CAD,
∴AE:CD=AD:CA=1:2,
∴CD=2AE=14 9
CF=
CD=6 7
,4 3
故答案为:
.4 3
