问题
解答题
已知向量
(1)若λ=2,α=
(7)若|
|
答案
(1)若λ=2,α=
,则π 3
=(1,OA
),3
=(1+sinβ,-cosβ),BC
由
⊥OA
,得:1+sinβ-BC
cosβ=0,即1+2sin(β-3
)=0,π 3
所以sin(β-
)=-π 3
,因为-1 2
<β-π 3
<π 3
,所以β-2π 3
=-π 3
,所以β=π 6
.π 6
(2)若|
|≥2|AB
|对任意实数α,β都成立,则(λcosα+sinβ)2+(λsinα-cosβ)2≥4对任意实数α,β都成立,OB
即λ2+1+2λsin(β-α)≥4对任意实数α,β都成立,
所以,
或λ>0 λ2+1-2λ≥4
,解得:λ≥3或λ≤-3,λ<0 λ2+1+2λ≥4
所以实数λ的取值范围是(-∞,-3]∪[3,+∞).

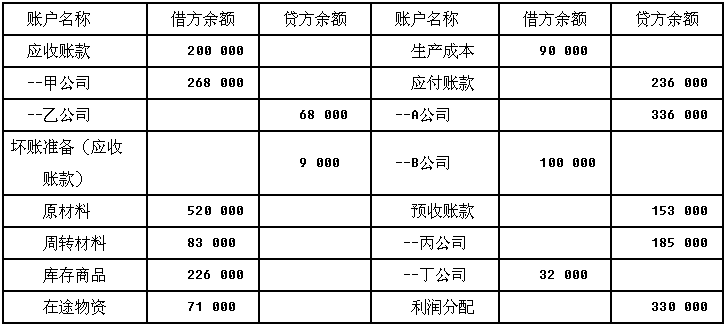 根据上表资料填列的资产负债表中,“应收账款”项目的期末余额为()元。
根据上表资料填列的资产负债表中,“应收账款”项目的期末余额为()元。