如图所示，电阻可忽略不计的光滑水平轨道，导轨间距L=1m，在导轨左端接阻值R=0.3Ω的电阻。在导轨框内有与轨轨平面垂直的有界匀强磁场，磁场边界为矩形区域cdef，其中cd、ef与导轨垂直，磁场宽度刚好等于轨轨间距L，磁场长度s=1m，磁感应强度B=0.5T。一质量为m=1kg，电阻r="0.2" Ω的金属导体棒MN垂直放置于导轨上，且与导轨接触良好。现对金属棒施以垂直于导轨的水平外力F，金属棒从磁场的左边界cd处由静止开始以加速度a=0.4m/s2作匀加速运动。
(1) 推导出水平拉力F随时间t变化的关系式；
(2) 力F作用一段时间t1后撤去力F；若已知撤去F后金属棒的速度v随位移x的变化关系为
(v0为撤去F时金属棒速度)，并且金属棒运动到ef处时速度恰好为零，则外力F作用的时间t1为多少？
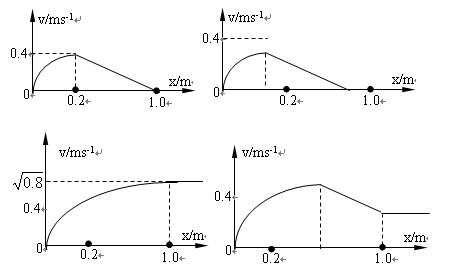
(3) 若在金属棒离开磁场区域前撤出外力F，试定性画出棒在整个运动过程中速度随位移变化所对应的各种可能的图线．(直接画图，不需要进行有关推导)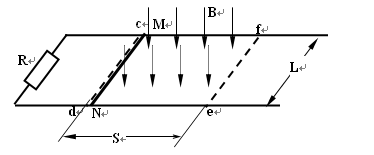
⑴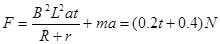
⑵t="1s(3)" 各种可能图形如下
⑴ 金属棒作匀加速运动，t时刻的速度V=at (1分)
金属棒速度V时回路中的感应电流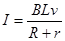
(1分)
金属棒中电流为I时受到的安培力F安=BIL (1分)
由牛顿第二定律知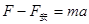
(1分)
所以拉力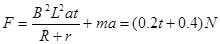 (2分)
⑵ 设F的作用时间为t，在该时间内
金属棒达到的速度V0=at=0.4t (1分)
金属棒的位移
(1分)
由题意给定关系式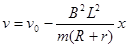
知撤去力F到停止运动的位移x2
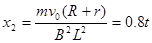(1分)
又根据题意知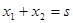
(1分)
由以上几式可解得t=1s (2分)
⑶ 各种可能图形如下。(每个图1分)