D  

题目分析：∵奇函数y=f（x）在[－1，0]上为单调递减函数，∴f（x）在[0，1]上为单调递减函数，∴f（x）在[-1，1]上为单调递减函数。

又α、β为锐角三角形的两内角

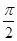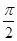∴α+β＞ ，∴α＞－β

∴sinα＞sin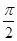（－β）=cosβ＞0

∴f（sinα）＜f（cosβ）

故选D。

点评：小综合题，利用奇函数的性质确定f（x）在[-1，1]上为单调递减函数。利用诱导公式得到sinα＞sin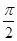（－β）=cosβ＞0 。