问题
解答题
用反证法证明(填空):
两条直线被第三条直线所截.如果同旁内角互补,那么这两条直线平行.
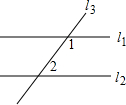
已知:如图,直线l1,l2被l3所截,∠1+∠2=180°.
求证:l1______l2
证明:假设l1______l2,即l1与l2交与相交于一点P.
则∠1+∠2+∠P______180°______
所以∠1+∠2______180°,这与______矛盾,故______不成立.
所以______.
答案
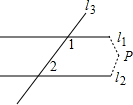
证明:假设l1不平行l2,即l1与l2交与相交于一点P.
则∠1+∠2+∠P=180°(三角形内角和定理),
所以∠1+∠2<180°,
这与∠1+∠2=180°矛盾,故假设不成立.
所以结论成立,l1∥l2.
