如图是一种磁动力电梯示意图。在竖直方向有两组很长的平行轨道PQ、MN，轨道间有水平方向、交替排列的匀强磁场B1和B2，B1=B2=1.0T，B1和B2的方向相反，两磁场始终竖直向上做匀速直线运动。电梯轿厢固定在如图所示的金属框abcd内（图中轿厢未画出）并与之绝缘。已知电梯满载时连同金属框的总质量为2.35×103kg，所受阻力f=500N，金属框垂直轨道的边长Lcd=2.0m，两磁场的竖直宽度均与金属框的高Lad相同，金属框整个回路的电阻R=2.0×10-3Ω，取g=10m/s2。假如设计要求电梯满载时能以v1=3.0m/s的速度匀速上升，求：
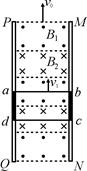
（1）图示时刻（ab边在磁场B1中，dc边在磁场B2中）金属框中感应电流的大小及方向（方向用顺时针或逆时针表示）；
（2）磁场向上运动速度v0的大小；
（3）该电梯满载以速度v1向上匀速运动时所消耗的总功率。
（1）
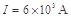感应电流沿逆时针方向 （2）
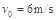（3）
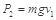
（1）因金属框匀速运动，所以金属框受到的安培力FB、重力G与阻力f之合力为零，设当电梯向上匀速运动时金属框中感应电流大小为I，则：
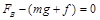…………………①
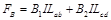…………………②
联解①②得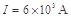： …………………③
感应电流沿逆时针方向 …………………④
（2）根据电流电方向可知:
v0>v1 …………………⑤
对金属框，由法拉第电磁感应定律和欧姆定律有：
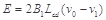…………………⑥
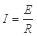…………………⑦
联解③⑥⑦得：
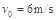…………………⑧
（3）金属框中的热功率为：
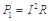…………………⑨
克服重力做功的功率为：
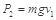…………………⑩
克服阻力的功率为：
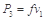…………………⑾
电梯消耗的总功率为：
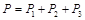…………………⑿
联解⑨⑩⑾⑿得：
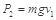…………………⒀