弹性势能是发生形变的物体所具有的能量.弹性势能跟形变的大小有关,例如弹簧的弹性势能跟弹簧被拉伸或压缩的长度(即形变量)有关,形变量越大,恢复原状时对外做的功越多,弹簧的弹性势能就越大.弹性势能跟形变量之间应该是怎样的定量关系呢?甲和乙两位同学为了解决这个问题,在实验室进行了探究弹簧压缩时具有的弹性势能与压缩量之间的关系的实验.以下是两位同学经历的一些实验探究过程,请你根据题目要求回答问题.
(1)甲同学在实验前提出了如下猜想:动能是物体运动具有的能量,动能的大小与运动速度有关,且跟运动速度的平方成正比,弹性势能是物体发生形变具有的能量,弹性势能的大小与形变有关,由此可以猜想弹性势能的大小也应该是跟形变量的平方成正比的关系.乙同学根据所学的物理知识用图象法从理论上证实了甲同学的猜想,他所用到的物理知识是:①弹簧发生形变时弹力与形变量的关系F=kx,②克服弹簧的弹力所做的功等于弹簧弹性势能的增加.请你完成甲同学的证明过程.
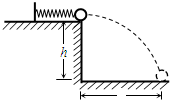
(2)两位同学为了用实验来证实他们的猜想,设计了如图所示的实验装置.在离地面高度为h的光滑水平桌面上,沿着与桌子边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的一小钢球接触.当弹簧处于自然长度时,小钢球恰好在桌子边缘.让钢球向左压缩弹簧一段距离后由静止释放,使钢球沿水平方向射出桌面,小球在空中飞行后落到水平地面,水平距离为s.为了完成实验,还需下列哪些器材?
A.秒表 B.刻度尺 C.白纸
D.复写纸 E.小球 F.游标卡尺
答:______.
(3)如果在实验中,得到弹簧压缩量x和小球离开桌面后的水平位移s的一些数据如下表:
| 实验次序 | 1 | 2 | 3 | 4 |
| x/cm | 2.00 | 3.00 | 4.00 | 5.00 |
| s/cm | 10.20 | 15.14 | 20.10 | 25.30 |
(1)画出F=kx图象,如图所示:
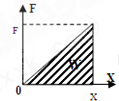
若将弹簧在外力作用下从原长(x=0)缓慢压缩x,此过程中外力克服弹力做功w即为图中阴影的面积,
即w=
Fx=1 2
kx21 2
克服弹簧的弹力所做的功等于弹簧弹性势能的增加.
所以弹簧压缩x所具有的弹性势能为:Ep=
kx2∝x21 2
(2)利用刻度尺测量小球的水平位移和弹簧的形变量,利用白纸和复写纸记录小球的落地点.故还需要刻度尺、白纸和复写纸.
故选BCD
(3)从实验数据可以得到:小球离开桌面的水平位移s跟弹簧的压缩量x成正比,即s∝x
小球在轨道上弹出的过程中,机械能守恒:Ep=
mv21 2
(m为小球的质量,v是小球离开轨道时的速度)
小球离开轨道后做平抛运动,则有:s=vt
h=
gt2 (h是轨道的B端离地面的高度)1 2
联立解得:Ep=
s2∝s2mg 4h
由s∝x,故有:Ep∝x2
故答案为:(1)证明过程在上.
(2)BCD
(3)弹性势能Ep与弹簧的压缩量x的关系为Ep∝x2
