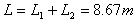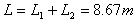问题
计算题
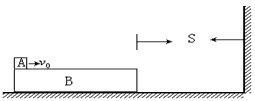
如图示，质量M=2kg的长木板B静止于光滑水平面上，B的右边放有竖直固定挡板，B的右端距离挡板S。现有一小物体A（可视为质点）质量为m=1kg，以初速度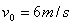
从B的左端水平滑上B。已知A与B间的动摩擦因数
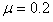，A始终未滑离B，B与竖直挡板碰前A和B已相对静止，B与挡板的碰撞时间极短，碰后以原速率弹回。求：
（1）B与挡板相碰时的速度大小；
（2）S的最短距离；
（3）木板B的长度L至少要多长。（保留2位小数）
答案
解：（1）设B与挡板相碰时的速度大小为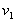
，由动量守恒定律
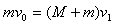
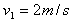
（2）A与B刚好共速时B到达挡板S距离最短，由牛顿第二定律，B的加速度
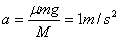
（3）A滑上B至B与挡板相碰过程中，A、B间的相对位移为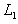
，根据动能定理，有
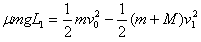
解得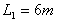
B与挡板碰后，A、B最后一起向左运动，共同速度大小为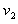
，由动量守恒定律
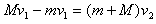
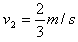
此过程中A、B的相对位移为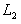
，则有
