问题
填空题
| 给出以下四个命题: ①若0<α<
②若
③若
④若π<α<
其中正确的命题序号是______. |
答案
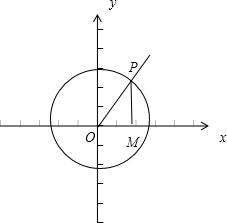
作出单位圆,作出∠α的正弦线MP和余弦线OM,
则sinα+cosα=MP+OM,所以:
①若0<α<
,此时角的终边在第一象限,则sinα+cosα=OM+MP>OP+1,故①是真命题;π 2
②若
<α<π,则sinα+cosα=OM+MP,此时角的终边在第二象限π 2
有-1<OM+MP<1,∴-1<sinα+cosα<1,故②是真命题;
③若
<α<2π,则sinα+cosα=OM+MP,此时角的终边在第四象限3π 2
有-1<OM+MP<1,∴-1<sinα+cosα<1,故③是真命题;
④若π<α<
,则角的终边在第三象限,则sinα+cosα=OM+MP,3π 2
有OM+MP<-1,∴sinα+cosα<-1,故④是真命题.
故答案为:①②③④.
