问题
计算题
如图（a）所示，一端封闭的两条足够长平行光滑导轨固定在水平面上，相距L，其中宽为L的abdc区域无磁场，cd右段区域存在匀强磁场，磁感应强度为B0,磁场方向垂直于水平面向上；ab左段区域存在宽为L的均匀分布但随时间线性变化的磁场B，如图（b）所示，磁场方向垂直水平面向下。一质量为m的金属棒ab，在t=0的时刻从边界ab开始以某速度向右匀速运动，经时间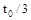
运动到cd处。设金属棒在回路中的电阻为R，导轨电阻不计。
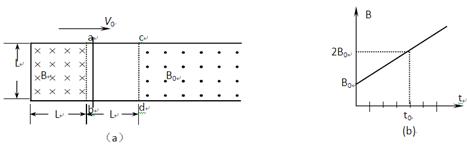
（1）求金属棒从边界ab运动到cd的过程中回路中感应电流产生的焦耳热量Q;
（2）经分析可知金属棒刚进入cd右段的磁场时做减速运动，求金属棒在该区域克服安培力做的功W。
答案
(1) 
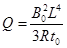(2) 
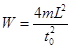
题目分析：(1)金属棒从ab运动到cd的过程中，感应电动势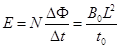
感应电流大小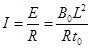
根据焦耳定律产生的热量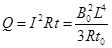
(2)金属板进入cd段的初速度为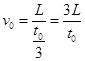
金属杆一旦进入cd段，一方面整个电路中左部分会产生感生电动势，还是和原来一样
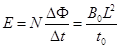感应电流方向根据楞次定律判断得金属棒中是由下向上；
同时金属棒切割磁感应线，也要产生动生电动势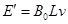
，
感应电流方向金属棒中由上向下，与动生电动势相反，
题中说，一开始减速，说明开始时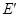
较大，总体感应电流金属棒中还是由上向下，才能与减速相符合，
随着速度的减小，会达到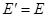
，此时电路中感应感应电流为零，金属棒不再减速，并将维持这个状态一直做匀速直线运动，于是我们可以求出做匀速直线运动的速度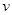
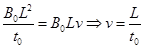
根据动能定理有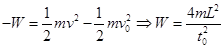
点评：本题要注意感生电动势和动生电动势都要考虑，电路中总的电动势当它们的方向相同时则相加，方向相反时则相减。