问题
解答题
求函数y=sin2x+2sinxcosx+3cos2x的最小值,并求使y取最小值时x的集合.
答案
当{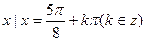 }时,函数取得最小值,最小值为2-
}时,函数取得最小值,最小值为2-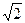
由y=sin2x+2sinxcosx+3cos2x
得:y=2sinxcosx+2cos2x+1 ="sin2x+cos2x" +2
=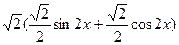 +2
+2
=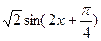 +2
+2
当 =" "
=" "  即x=
即x=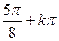 时,
时, y=2-
y=2-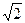
所以当{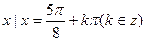 }时,函数取得最小值,最小值为2-
}时,函数取得最小值,最小值为2-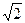 .
.
求函数y=sin2x+2sinxcosx+3cos2x的最小值,并求使y取最小值时x的集合.
当{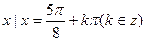 }时,函数取得最小值,最小值为2-
}时,函数取得最小值,最小值为2-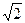
由y=sin2x+2sinxcosx+3cos2x
得:y=2sinxcosx+2cos2x+1 ="sin2x+cos2x" +2
=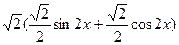 +2
+2
=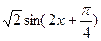 +2
+2
当 =" "
=" "  即x=
即x=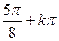 时,
时, y=2-
y=2-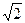
所以当{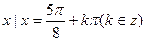 }时,函数取得最小值,最小值为2-
}时,函数取得最小值,最小值为2-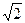 .
.