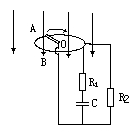
如图所示,在磁感强度B= 2T的匀强磁场中,有一个半径r=0.5m的金属圆环。圆环所在的平面与磁感线垂直。OA是一个金属棒,它沿着顺时针方向以20rad/s的角速度绕圆心O匀速转动。A端始终与圆环相接触OA棒的电阻R=0.1Ω,图中定值电阻R1=100Ω,R2=4.9Ω,电容器的电容C=100pF。圆环和连接导线的电阻忽略不计,求:
(1)电容器的带电量。哪个极板带正电。
(2)电路中消耗的电功率是多少?
(1)上板(2)5W
【错解分析】错解:
(1)由于电容器两板间分别接在做切割磁感线导体棒的两端,电容器两端的电压就等于导体OA上产生的感应电动势。
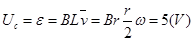
根据电容器的定义 ,则
,则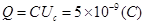
根据右手定则,感应电流的方向由O→A,故电容器下板由于与O相接为正,上极板与A相接为负。
(2)根据闭合电路欧姆定律

电路中消耗的电功率P消=I2R=4.9(W)
(1)电容器两板虽然与切割磁感线的导体相连,但两板间并不等于导体棒OA产生的感应电动势。因为导体棒有电阻。所以电容器的电压应等于整个回路的端电压。
(2)电路中消耗的功率由于导体棒有电阻,即相当于电源有内阻,所以电路中消耗的功率不仅在外电阻R2上,而且还消耗在内阻R上。P消=I2(R+R2)或根据能量守恒P源=Iε。
【正解】(l)画出等效电路图,图所示。

导体棒OA产生感应电动势
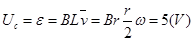

则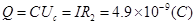
根据右手定则,感应电流的方向由O→A,但导体棒切割磁感线相当于电源,在电源内部电流从电势低处流向电势高处。故A点电势高于O点电势。又由于电容器上板与A点相接即为正极,同理电容器下板由于与O相接为负极。
(2)电路中消耗的电功率P消=I2(R+R2)=5(W),或P消=Iε=5(W)
