(1) 1A (2)3.6m/s(3) 能的转化符合守恒定律

题目分析：(1)对AB，受力分析如图，当AB所受合外力为零时，AB速度达到稳定且最大。

此时f=F=BIL      ①(1分)

I=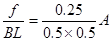=1A   ②(2分)

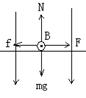
(2)设AB最大速度为V，此时AB切割磁感线产生的电动势为E'，

依法拉第电磁感应定律得：E'="BLV"       ③ (1分)

依全电路欧姆定律得：I=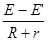      ④  (1分)

由③④得:V=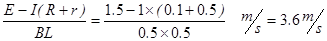  ⑤(2分)

(3)导体AB速度达最大后，电源消耗的电能转化为回路的电热和AB与金属框摩擦产生的内能。          ⑥   (1分)

电源消耗的功率：

P=IE=1×1.5W=1.5W           ⑦    (1分)

回路产生的热功率：

P热="I2(R+r)=12×(0.1+0.5)W=0.6W"      ⑧    (1分)

AB克服摩擦力做功的功率：

P'=fV=0.25×3.6W=0.9W           ⑨(1分)

由⑦⑧⑨可知，P= P热+P'。

可见，能的转化符合守恒定律            ⑩(1分)

点评：做此类型的关键是对导体棒运动分析，根据闭合回路欧姆定律分析解题