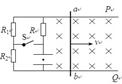
如图，光滑的平行导轨P、Q相距L="1" m，处在同一水平面中，导轨的左端接有如图所示的电路，其中水平放置的电容器两极板相距d="10" mm，定值电阻
，
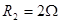，导轨的电阻不计。磁感应强度B=0.4T的匀强磁场竖直向下穿过导轨面。当金属棒ab沿导轨向右匀速运动（开关S断开）时，电容器两极板之间质量
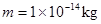、带电荷量
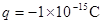的微粒恰好静止不动；当S闭合后，微粒以a="7" m/s2向下做匀加速运动。取g="10" m/s2。求：
（1）金属棒ab运动的速度大小是多大?电阻是多大?
（2）闭合后，使金属棒ab做匀速运动的外力的功率是多大?
（1）v="3" m/s，r=2Ω（2）0.18 W
题目分析：（1）带电微粒在电容器两极间静止时，受向上的电场力和向下的重力作用而平衡，即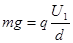
由此式可解出电容器两极板间的电压为
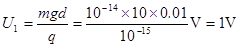
由于微粒带负电，可知上板的电势高。
由于S断开，R1、R2的电压和等于电容器两端电压U1，R3上无电流通过，可知电路中的感应电流即为通过R1、R2的电流I1，
从而ab切割磁感线运动产生的感应电动势为
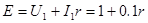①
S闭合时，带电微粒向下做匀加速运动，由牛顿第二定律可得
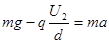
所以有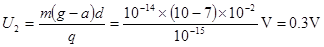 
此时的感应电流为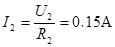
由闭合电路欧姆定律可得
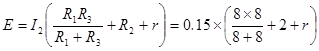②
解①②两式可得E="1.2" V, r="2" Ω
由E=BLv可得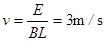
即导体棒ab匀速运动的速度v="3" m/s，电阻r=2Ω
（2）S闭合时，通过ab的电流I2="0.15" A，ab所受的安培力为F2=BI2L="0.06" N
ab以速度v="3" m/s做匀速运动，所受外力F必与磁场力F2大小相等、方向相反，即
F="0.06" N，方向向右。
可见，外力的功率为 P=Fv="0.06×3" W="0.18" W
点评：在电磁感应现象中，产生感应电动势的那部分电路相当于电源．