搜题请搜索小程序“爱下问搜题”
问题 填空题
关于平面向量
a
，
b
，
c
，有下 * * 个命题：
①若
a
•
b
=
a
•
c
，则
b
=
c
、
②若
a
=（1，k），
b
=（-2，6），
a
∥
b
，则k=-3．
③非零向量
a
和
b
满足|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
+
b
的夹角为60°．
其中真命题的序号为______．（写出所有真命题的序号）
答案

①若

a
•
b
=
a
•
c
，则
a
•（
b
-
c
）=0，此时
a
⊥（
b
-
c
），而不一定
b
=
c
，①为假．

②由两向量

a
∥
b
的充要条件，知1×6-k•（-2）=0，解得k=-3，②为真．

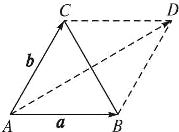
③如图，在△ABC中，设

AB
=a，
AC
=b，
CB
=a-b，

由|

a
|=|
b
|=|
a
-
b
|，可知△ABC为等边三角形．

由平行四边形法则作出向量

a
+
b
=
AD
，

此时

a
与
a
+
b
成的角为30°．③为假．

综上，只有②是真命题．

答案：②

多项选择题

超过校核洪水的应急调度方案应包括：（）调度方案，并报上级主管部门审批。

A.模拟超过校核洪水过程

B.模拟超过设计洪水过程

C.配合枢纽工程应急防洪抢险的措施

D.配合生活区应急防洪抢险的措施
查看答案
单项选择题 A1/A2型题

以下关于国际非专利名叙述不正确的是（）

A.被全球公认且属公共财产，也称之为通用名称

B.是WHO为每一种药品制定的唯一名称

C.应避免采用单个字母和数字

D.应避免采用可能给患者以有关解剖学、生理学、病理学或治疗学暗示的名称

E.其发音和拼法应清晰明了
查看答案