问题
计算题
(14分)如图所示,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l="0.2" m,在导轨的一端接有阻值R="3" Ω的电阻,在x≥0处有一垂直水平面向下的匀强磁场,磁感强度B="0.5" T。一质量m ="0." 1kg,电阻r="2" Ω的金属棒垂直搁在导轨上,并以v0="20" m/s的初速度进入磁场,在水平拉力F的作用下作匀减速直线运动,加速度大小a="2" m/s2。棒与导轨接触良好,其余电阻均不计。求:

(1)第一次电流为零时金属棒所处的位置;
(2)电流第一次减少为最大值的一半时拉力F的大小及其功率;
(3)金属棒开始进入磁场到速度减小为零的过程中,电阻R上产生的热量为1.6 J,求该过程中拉力F所做的功。
答案
(1) (2)
(2) 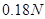
 (3)
(3) 
题目分析:本题是电磁感应与力学知识的综合,安培力是联系这两部分的桥梁.
(1)由法拉第电磁感应律得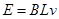 ,根据闭合电路欧姆定律有
,根据闭合电路欧姆定律有 ,于是可知电流与速度成正比,当电流第一次为零时,金属棒的速度为零,即
,于是可知电流与速度成正比,当电流第一次为零时,金属棒的速度为零,即 时,
时,
根据运动学公式得第一次电流为零时金属棒通过的位移为

(2)金属棒刚开始运动时,回路中电流最大,根据闭合电路欧姆定律得最大电流为
若 ,则金属棒的速度
,则金属棒的速度
则金属棒所受的安培力为
可知
又根据牛顿第二定律得
故
则功率为
(3)设金属棒克服安培力做功为 ,拉力做功为
,拉力做功为 ,由动能定理可知:
,由动能定理可知:
金属棒开始进入磁场到速度减小为零的过程中,电阻R上产生的热量为 ,则根据焦耳定律知回路中产生的总热量为
,则根据焦耳定律知回路中产生的总热量为
根据功能关系知,回路中产生的焦耳热等于金属棒克服安培力做功,则得

联立以上各式解得
