（1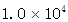）Pa    （2）200     （3）0.3m

题目分析：当A的表面刚没入水面时，知道底部所处的深度，根据p=ρgh求出底部受到水的压强；当物块A的顶部刚没入水面时，知道物块A的底面积和高，可求出物块A的体积，由于是没入，所以排开液体的体积求出来了，根据F_浮=ρ_水V_排g求出物块A受到的浮力，再根据F_拉=G_A-F_浮求出物块A受到的拉力；先根据F_示=G_B-F_N，求出杠杆N端受到的拉力，根据杠杆的平衡条件求出杠杆M端受到的拉力；根据动滑轮的特点求出滑轮组对A的拉力；然后根据阿基米德定律的变形公式求出排开液体的体积，用体积除以底面积求出深度。

（1）当物块A的顶部刚没入水面时，底部所处的深度：

h=1m，

底部受到水的压强：

p=ρgh=1×10³kg/m³×10N/kg×1m=1×10⁴Pa．

（2）物块A的体积：

V_A=0.04m²×1m=0.04m³，

物体A重：

G_A=ρ_AV_Ag=1.5×10³kg/m³×0.04m³×10N/kg=600N，

∵物块A没入水中，

∴排开水的体积：

V_排=V_A=0.04m³，

物块A所受的浮力：

F_浮=ρ_水V_排g=1×10³kg/m³×0.04m³×10N/kg=400N；

物块A所受的拉力：

F_拉=G_A-F_浮=600N-400N=200N；

（3）①电子秤的示数F_示=G_B-F_N，则杠杆N端受到的拉力：

F_N=G_B-F_示=100N-40N=60N，

∵杠杆平衡，MO：ON=1：2

∴F_ML_OM=F_NL_ON，

∴杠杆M端受到的拉力：

F_M=120N；

②滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计，

滑轮D受到向下的拉力：

F_D=2F_M=2×120N=240N，

滑轮C受到向下的拉力：

F_C=2F_D=2×240N=480N，

∴滑轮组对A的拉力：

F_拉A=F_C=480N；

③∵F_拉A+F_浮=G_A，

∴F_浮=G_A-F_拉A=ρ_AV_Ag-F_拉A=1.5×10³kg/m³×0.04m³×10N/kg-480N=600N-480N=120N，

∵F_浮=ρ_水V_排g，

∴，

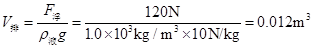∵V_排=Sh_浸，

∴物块A浸入水中的深度：

h_浸=

点评：此题是一道综合性试题，结合浮力的计算和杠杆的平衡条件等知识点，难度较大