问题
填空题
| 已知命题： ①函数f(x)=
②定义在R上的函数f（x）在区间（-∞，0]上是单调减函数，在区间（0，+∞）上也是单调减函数，则函数f（x）在R上是单调减函数； ③函数f（x）=loga（x-1）+3的图象一定过定点； ④函数y=|3-x2|的图象和函数y=a的图象的公共点个数为m，则m的值不可能是1． 其中正确命题的序号为______． |
答案
①因为函数f（x）的图象关于y轴对称，所以函数f（x）是偶函数，所以①正确．
②若f(x)=
满足条件，但函数在R上不单调，所以②错误．-x，x≤0 -x+1，x＞0
③当x=2时，f（2）=loga（2-1）+3=3，所以函数f（x）=loga（x-1）+3的图象一定过定点（2，3），所以③正确．
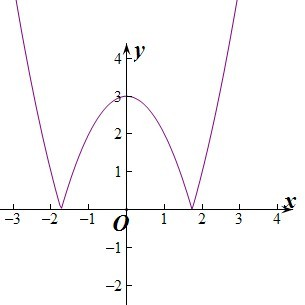
④作出函数y=|3-x2|的图象如图：
由图象可知函数为偶函数，所以函数y=|3-x2|的图象和函数y=a的图象的公共点个数为0个或4个或3个或2个，所以则m的值不可能是1个，所以④正确．
故答案为：①③④．