问题
计算题
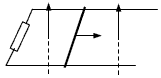
如图所示，一对平行光滑轨道放置在水平面上，两轨道相距L=1m，两轨道之间用电阻R=2Ω连接，有一质量为m=0.5kg的导体杆静止地放在轨道上与两轨道垂直，杆及轨道的电阻皆可忽略不计，整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直轨道平面向上。现用水平向右拉力沿轨道方向拉导体杆，使导体杆从静止开始做匀加速运动。经过位移s=0.5m后，撤去拉力，导体杆又滑行了s'=3s=1.5m后停下。求：
（1）全过程中通过电阻R的电荷量；
（2）整个过程中导体杆的最大速度；
（3）在匀加速运动的过程中，某时拉力与时间的关系式。
答案
解：（1）设全过程中平均感应电动势为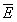
，平均感应电流为
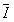，时间为
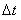，通过电阻R的电荷量为q
则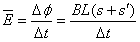
=
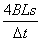
得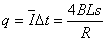
=2C
（2）拉力撤去时，导体杆的速度v即为最大速度，拉力撤去后杆运动时间为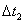
，平均感应电流为
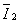，根据动量定理有：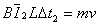
即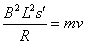
，
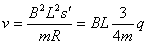=6m/s
（3）匀加速运动过程中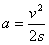
=36m/s2
对t时刻，由牛顿运动定律得F－BIL=ma
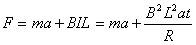=0.5×36+
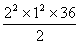t=18+72t