由f（-x+2）=f[-（x-2）]，所以函数y=f（-x+2）的图象是把函数y=f（-x）的图象向右平移2个单位得到的，

y=f（x-2）的图象是把y=f（x）的图象向右平移2个单位得到的，而y=f（x）与y=f（-x）的图象关于y轴轴对称，

所以，函数y=f（-x+2）与y=f（x-2）的图象关于直线x=2对称．所以，命题①错误；

令x²+2x=t，则函数函数y=(

1

2

)x2+2x化为y=(

1

2

)t，又t=x²+2x=（x+1）²-1≥-1，

0＜(

1

2

)t≤2，即函数y=(

1

2

)x2+2x的值域是（0，2]．所以命题②错误；

函数f（x）=log_a|x|（a＞0，a≠1）在（0，+∞）上单调递增，因为t=|x|在（0，+∞）上单调递增，所以，

函数y=log_at也在（0，+∞）上单调递增，则a＞1，a+1＞2．又因为函数f（x）=log₂|x|是偶函数，

所以f（-2）=f（2），则f（-2）=f（2）＜f（a+1）．所以，命题③错误；

由f（x）=

(3a-1)x+4a，(x＜1) logax，(x≥1)

是（-∞，+∞）上的减函数，则

3a-1＜0 0＜a＜1 (3a-1)+4a≥loga1

，

解得：

1

7

≤a＜

1

3

．所以，命题④错误；

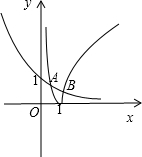
令y1=2-x，y₂=|lgx|，

在平面直角坐标系中作出这两个函数的图象如图，

不妨设A点的横坐标为x₁，B点的横坐标为x₂，则x₁＜1＜x₂，

由

1

2x1

=|lgx1|=-lgx1，得lgx1=-

1

2x1

，

lgx2=|lgx2|=

1

2x2

，得：lgx1x2=lgx1+lgx2=

1

2x2

-

1

2x1

=

2x1-2x2

2x12x2

＜0．

所以，0＜x₁x₂＜1．所以，命题⑤正确．

故答案为⑤．