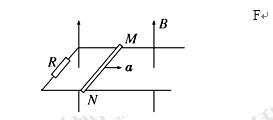
（10分）如图所示，一对光滑的平行金属导轨固定在同一水平面内，导轨间距L=0.5m，左端接有阻值R=0.3Ω的电阻，一质量m=0.1kg，电阻r=0.1Ω的金属棒MN放置在导轨上，整个装置置于竖直向上的匀强磁场中，磁场的磁感应强度B=0.4T，棒在水平向右的外力作用下，由静止开始做匀加速直线运动，当棒运动的位移x=9m时速度达到6m/s，此时撤去外力，棒继续运动一段距离后停下来，已知撤去外力前后回路中产生的焦耳热之比Q1：Q2=2:1，导轨足够长且电阻不计，棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触，求
(1) 棒在匀加速运动过程中，通过电阻R的电荷量q
(2) 金属棒MN做匀加速直线运动所需外力随时间变化的表达式
(3) 外力做的功WF
（1）4.5C（2）F＝0.2＋0.2t （3）5.4J
题目分析：（1）设棒匀加速运动的时间为Δt，回路的磁通量变化量为ΔΦ，回路中的平均感应电动势为，由法拉第电磁感应定律得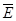
＝
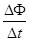
其中ΔΦ＝Blx
设回路中的平均电流为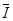
，由闭合电路的欧姆定律得＝
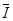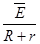
则通过电阻R的电荷量为q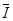＝Δ
联立①②③④式，代入数据得q＝4.5 C
（2）)设撤去外力时棒的速度为v，对棒的匀加速运动过程，由运动学公式v2＝2ax
得a＝2 m/s2
E＝Blv
I=E/(R+r)
由安培力公式和牛顿第二定律得F－BIl＝ma
得F＝0.2＋0.2t
（3）撤去外力后棒在安培力作用下做减速运动，安培力做负功先将棒的动能转化为电能，再通过电流做功将电能转化为内能，所以焦耳热等于棒的动能减少。有
Q2=ΔEK=mv2/2=1.8J
根据题意在撤去外力前的焦耳热为Q1= Q2=3.6J
撤去外力前拉力做正功、安培力做负功（其大小等于焦耳热Q1）、重力不做功共同使棒的动能增大，根据动能定理有ΔEK=WF-Q1
则ΔEK=WF=Q1+ΔEK=5.4J