问题
选择题
| 给出下列四个命题: ①若|
②在△ABC中,若
③若
④若
其中,正确命题的个数是( )
|
答案
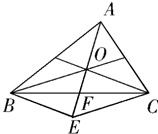
证明:①若|
|+|a
|=0,则|b
|=|a
|=0,则b
=a
=b
;0
正确;
对于②:如图,延长AO到E,
使OE=AO,交BC于F,
则
=-OE
.OA
而由
+OA
+OB
=0,OC
有
+OB
=-OC
,∴OA
+OB
=OC
,OE
∴四边形OBEC为平行四边形.
∴OE平分BC,即AO所在的直线为△ABC的边BC上的中线.
同理可证,CO,BO所在的直线分别为AB,AC边上的中线.∴O为△ABC的重心.正确;
对于③:若
,a
是共线向量,则它们的夹角θ为0或π,则b
•a
=|b
|•|a
|cosθ=±|b
|•|a
|,故③错;b
④若
,a
是非零向量,若存在非零向量b
,使c
•a
+c
•b
=(c
+a
)•b
=0,说明向量(c
+a
)与b
垂直,并不能得出c
+a
=b
,故错.0
故选B.
