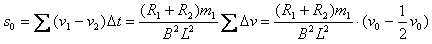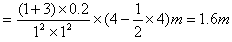问题
计算题
如图所示,两根足够长的平行金属导轨由倾斜和水平两部分平滑连接组成,导轨间距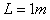 ,倾角θ=45°,水平部分处于磁感应强度
,倾角θ=45°,水平部分处于磁感应强度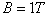 的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒
的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直。金属棒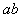 质量
质量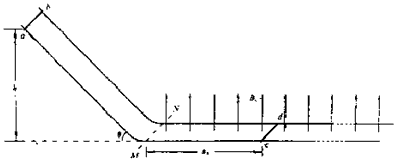 ,电阻
,电阻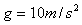 ,金属棒
,金属棒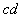 质量
质量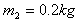 ,电阻
,电阻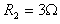 ,导轨电阻不计,两棒与导轨间动摩擦因数
,导轨电阻不计,两棒与导轨间动摩擦因数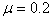 。开始时,棒
。开始时,棒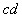 放在斜导轨上,与水平导轨高度差
放在斜导轨上,与水平导轨高度差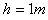 ,棒
,棒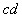 放在水平轨上,距MN距离为
放在水平轨上,距MN距离为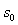 。两棒均与导轨垂直,现将棒
。两棒均与导轨垂直,现将棒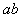 由静止释放,取
由静止释放,取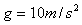 。求:
。求:
(1)棒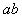 运动到MN处的速度大小;
运动到MN处的速度大小;
(2)棒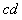 运动的最大加速度;
运动的最大加速度;
(3)若导轨水平部分光滑,要使两棒不相碰,棒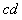 距离MN的最小距离
距离MN的最小距离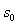 。
。

答案
解:(1)对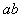 运用动能定理得
运用动能定理得
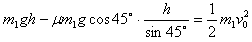

(2)棒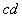 运动到MN处,
运动到MN处,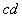 加速度最大
加速度最大
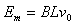 ,
,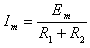
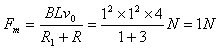
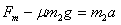
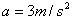
(3)在不相碰的情况下,两棒最终速度必相等,设为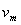
对棒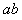 有
有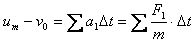
对棒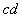 有
有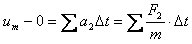
任一时刻有
故得
设某时刻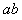 的速度为
的速度为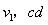 的速度为
的速度为 ,在极小的
,在极小的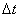 内,
内,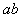 速度变化为
速度变化为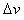
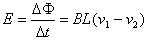 ,
,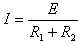
由牛顿运动定律有
得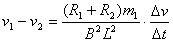
两棒在水平导轨运动的相对位移,即为两棒不相碰的最小距离,故有