问题
不定项选择
两根光滑的金属导轨,平行放置在倾角为θ斜面上,导轨的左端接有电阻R,导轨自身的电阻可忽略不计。斜面处在一匀强磁场中,磁场方向垂直于斜面向上。质量为m,电阻可不计的金属棒ab,在沿着斜面与棒垂直的恒力作用下沿导轨匀速上滑,并上升h高度,如图所示。在这过程中
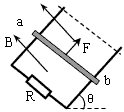
A.作用于金属捧上的各个力的合力所作的功等于零
B.作用于金属捧上的各个力的合力所作的功等于mgh与电阻R上发出的焦耳热之和
C.金属棒克服安培力做的功等于电阻R上发出的焦耳热
D.恒力F与重力的合力所作的功等于电阻R上发出的焦耳热
答案
ACD
解:A、B导体棒匀速上升过程中,合力为零,则合力所作的功等于零,根据动能定理得:WF-WG-W安=0,得WF=WG+W安,克服安培力所做功W安即等于回路电阻中产生的热量,故有:金属棒上的各个力的合力所做的功等于零,恒力F等于mgh与电阻R上发出的焦耳热之和,A正确,B错误;
C、根据功能关系可知,金属棒克服安培力做的功等于电阻R上发出的焦耳热.故C正确.
D、由WF-WG-W安=0得,WF-WG=W安,即恒力F与重力的合力所做的功等于克服安培力所做功,即等于电阻R上发出的焦耳热,故D正确.故选ACD.
