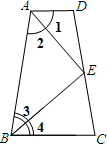
如图,凸四边形ABCD中,点E在边CD上,连接AE、BE.给出下 * * 个关系式:①AD∥BC;②DE=EC;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为已知条件、另外两个关系式作为结论,可以构成一些命题(下面各小题的命题须符合此要求).
(1)共计能够成______个命题;
(2)写出三个真命题:
①如果______、______、______,那么______、______;
②如果______、______、______,那么______、______;
③如果______、______、______,那么______、______.
请选择上述三个命题中的一个写出它是真命题的理由:
证明:我选择证明命题______(填序号),理由如下:
(3)请写出一个假命题(不必说明理由):
如果______、______、______,那么______、______.
列表如下:
| 序号 | 条件 | 结论 | 命题真假 | |||
| 1 | ③∠1=∠2 | ④∠3=∠4 | ⑤AD+BC=AB | ①AD∥BC | ②DE=EC | 真 |
| 2 | ②DE=EC | ④∠3=∠4 | ⑤AD+BC=AB | ①AD∥BC | ③∠1=∠2 | 真 |
| 3 | ②DE=EC | ③∠1=∠2 | ⑤AD+BC=AB | ①AD∥BC | ④∠3=∠4 | 真 |
| 4 | ②DE=EC | ③∠1=∠2 | ④∠3=∠4 | ①AD∥BC | ⑤AD+BC=AB | 假 |
| 5 | ①AD∥BC | ④∠3=∠4 | ⑤AD+BC=AB | ②DE=EC | ③∠1=∠2 | 真 |
| 6 | ①AD∥BC | ③∠1=∠2 | ⑤AD+BC=AB | ②DE=EC | ④∠3=∠4 | 真 |
| 7 | ①AD∥BC | ③∠1=∠2 | ④∠3=∠4 | ②DE=EC | ⑤AD+BC=AB | 真 |
| 8 | ①AD∥BC | ②DE=EC | ⑤AD+BC=AB | ③∠1=∠2 | ④∠3=∠4 | 真 |
| 9 | ①AD∥BC | ②DE=EC | ④∠3=∠4 | ③∠1=∠2 | ⑤AD+BC=AB | 真 |
| 10 | ①AD∥BC | ②DE=EC | ③∠1=∠2 | ④∠3=∠4 | ⑤AD+BC=AB | 真 |
(1)10;
(2)表中9个真命题选1,
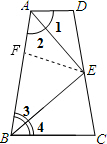
理由如下:如图,在AB上截取AF=AD,连接EF,
在△ADE和△AFE中,
,AD=AF ∠1=∠2 AE=AE
∴△ADE≌△AFE(SAS),
∴∠D=∠AFE,DE=EF,
∵AD+BC=AB,
∴BC=BF,
在△BCE和△BFE中,
,BC=BF ∠3=∠4 BE=BE
∴△BCE≌△BFE(SAS),
∴∠C=∠BFE,CE=EF,
∴DE=CE,
∵∠AFE+∠BFE=180°,
∴∠C+∠D=180°,
∴AD∥BC;
(3)假命题是:“如果DE=EC、∠1=∠2、∠3=∠4,那么AD∥BC、AD+BC=AB.”
