问题
计算题
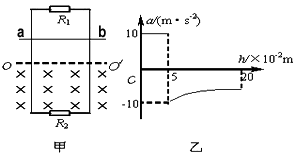
如图甲所示，平行金属导轨竖直放置，导轨间距为L=1m，上端接有电阻R1=3Ω，下端接有电阻R2=6Ω，虚线OO'下方是垂直于导轨平面的匀强磁场。现将质量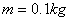
、电阻不计的金属杆ab，从OO'上方某处垂直导轨由静止释放，杆下落0.2m过程中始终与导轨保持良好接触，加速度a与下落距离h的关系图象如图乙所示。求：
（1）磁感应强度B；
（2）杆下落0.2m过程中通过电阻R2的电荷量q。
答案
解：(1)由图象知，杆自由下落距离是0.05m，当地重力加速度g＝10m/s2，则杆进入磁场时的速度v＝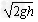
＝1m/s
由图象知，杆进入磁场时加速度a＝－g＝－10m/s2
由牛顿第二定律得mg－F安＝ma
回路中的电动势E＝BLv
杆中的电流I＝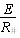
R并＝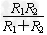
F安＝BIL＝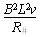
得B＝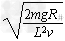
＝2T
(2)杆在磁场中运动产生的平均感应电动势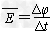
杆中的平均电流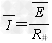
通过杆的电荷量Q＝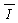
△t
通过R2的电量q＝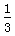
Q＝0.05C