顺次连接等腰梯形各边中点所得的四边形是菱形，理由为：

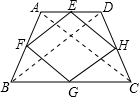
已知：等腰梯形ABCD，E、F、G、H分别为AD、AB、BC、CD的中点，

求证：四边形EFGH为菱形．

证明：连接AC，BD，

∵四边形ABCD为等腰梯形，

∴AC=BD，

∵E、H分别为AD、CD的中点，

∴EH为△ADC的中位线，

∴EH=

1

2

AC，EH∥AC，

同理FG=

1

2

AC，FG∥AC，

∴EH=FG，EH∥FG，

∴四边形EFGH为平行四边形，

同理EF为△ABD的中位线，

∴EF=

1

2

BD，又EH=

1

2

AC，且BD=AC，

∴EF=EH，

则四边形EFGH为菱形．

故答案为：菱形