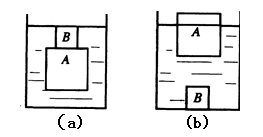
底面积为400cm2的圆柱形容器内装有适量的水,将其竖直放在水平桌面上,把边长为10cm的正方体木块A放入水后,再在木块A的上方放一物体B,物体B恰好没入水中,如图所示.已知物体B的密度为6×103kg/m3.质量为0.6kg.
求:(1)物体B的体积;
(2)木块A的密度;
(3)若将B放入水中,如图(b)所示,请分析出液面的变化情况;
(4)并求此时水对容器底部压强的变化值.
(1)0.1×10-3m3 ( 2) 0.5×103kg/m3 (3)将B放入水中后,A漂浮,有一部分体积露出水面,造成液面下降 (4)125Pa
题目分析:(1)物体B的体积 V=mB/ρB=0.6kg/6×103㎏/m3=1×10-4m3
(2)由图(a)A、B共同悬浮得:F浮A+F浮B=GA+GB
公式展开:p水g(VA+VB)=pA VAg+mBg
其中VA=(0.1m)3=1×10-3m3,把数据代入得:
1×103kg/m³× 10N/kg× 1×10-3m3+1×10-4m3)=pA×1×10-3m3 ×10N/kg+0.6kg ×10N/kg得:
pA=0.5103kg/m³
(3)将B放入水中后,A漂浮,有一部分体积露出水面,造成液面下降。
(4)A漂浮时F浮A=GA
p水gVA排=pA VAg得VA排=pA VA/p水=0.5×103kg/m³×10-3m3/1×103kg/m³=0.5×10-3m3
液面下降Δh=Δv/S=(VA-VA排)/S=(1×10-3m3-0.5×10-3m3)/0.04m2=0.0125m
减少的压强为Δp=p水gΔh=1×103kg/m³ ×10N/kg×0.0125m=125Pa
