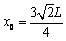如图所示，“×”型光滑金属导轨abcd固定在绝缘水平面上，ab和cd足够长，∠aOc=60°。虚线MN与∠bOd的平分线垂直，O点到MN的距离为L。MN左侧是磁感应强度大小为B、方向竖直向下的匀强磁场。一轻弹簧右端固定，其轴线与∠bOd的平分线重合，自然伸长时左端恰在O点。一质量为m的导体棒ef平行于MN置于导轨上，导体棒与导轨接触良好。某时刻使导体棒从MN的右侧L/4处由静止开始释放，导体在被压缩弹簧的作用下向左运动，当导体棒运动到O点时弹簧与导体棒分离。导体棒由MN运动到O点的过程中做匀速直线运动。导体棒始终与MN平行。已知导体棒与弹簧彼此绝缘，导体棒和导轨单位长度的电阻均为r0，弹簧被压缩后所获得的弹性势能可用公式
计算，k为弹簧的劲度系数，x为弹簧的形变量。
（1）证明：导体棒在磁场中做匀速直线运动的过程中，感应电流的大小保持不变；
（2）求弹簧的劲度系数k和导体棒在磁场中做匀速直线运动时速度v0的大小；
（3）求导体棒最终静止时的位置距O点的距离。
解：（1）设导体棒在磁场中做匀速直线运动时的速度为v0，某时刻导体棒在回路中的长度为l，则此时感应电动势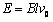
此时回路的电阻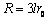
回路中的感应电流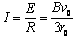
①
因为B、v0和r0均为不变量，所以感应电流I为不变量
（2）释放导体棒后，在未进入磁场的过程中，导体棒和弹簧组成的系统机械能守恒，则有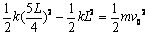
②
导体棒在磁场中做匀速直线运动的过程中，设某时刻导体棒距O的距离为x，根据牛顿第二定律有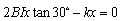
③
由①②③解得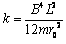
④
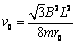⑤
（3）导体棒过O点后与弹簧脱离，在停止运动前做减速运动。设某时刻导体棒距O点的距离为x，导体棒在回路中的长度为l，加速度为a，速度为v，回路中的电流强度为I，根据牛顿第二定律有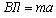
又因为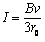
所以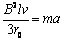
⑥
取一段很短的时间，导体棒在回路中的长度为l、加速度为a和速度为v，l、a和v可认为不变。设在这段时间内导体棒速度的变化量大小为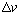
，回路所围面积的变化量为
。将⑥式左右两边同时乘以
，可得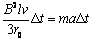
则导体棒从O点开始运动到静止的过程可表示为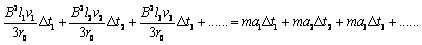
即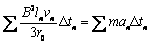
所以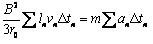
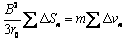
设导体棒最终静止的位置距O点的距离为x0，则
⑦
由⑤⑦式可解得