某实验小组用图1所示装置探究“重锤动能变化与重力对它做功的关系”。实验中，让拖着纸带的重锤从高处由静止自由落下，打点计时器在纸带上打出一系列的点，通过对打下的点进行测量和研究，即可达到实验目的．
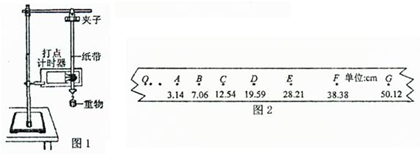
小题1: 图2是实验中打下的一条纸带，O点是重物开始下落时打下的起点，该小组在纸带上选取A、B、C、D、E、F、G七个计数点，每两个计数点间还有一个计时点（图中未画出），各计数点与起点O的距离如图所示，已知打点计时器工作频率为50Hz，分别计算B、C、D、E、F五个计数点与O点的速度平方差△v2（△v2= v2- v02）。其中D点应填的数据为： （保留3位有效数字）
| 计数点 | B | C | D | E | F |
| 速度平方差△v2/（m·s-1）2 | 1.38 | 2.45 | 5.52 | 7.50 |
小题3:重锤下落过程中一定受到阻力的作用。若已知当地的重力加速度为g，用这一装置测量重锤下落过程中受到的阻力F的大小，还需测量的物理量是 ， F大小的表达式为：F= （用符号表示）
小题1:3.84
小题2:9.78m/s2
小题3:重锤质量m，F= m(g-g’)
解：（1）计数点之间的时间间隔为T=0.04s，根据在匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，可以求出D点速度大小为：vD=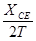
≈1.96m/s 所以△v2=
-0=3.83m2/s2，由于所取位移和时间不同，因此在3.83～3.84范围范围内均可以．故答案为：3.83（3.83～3.84）
（2）根据公式学公式v2=2gh，可知图象的斜率表示2g，由图象求出其斜率为k=19.56，所以当地的重力加速度为g=9.78m/s2，在9.67～9.94m/s2范围内均正确．故答案为：9.78m/s2（9.67～9.94m/s2）．
（3）根据牛顿第二定律有mg-f=mg′，可知，只要测量重锤的质量m，即可正确求出空气阻力大小．故答案为：重锤质量m．
根据牛顿第二定律有mg-F=mg′可以求出阻力的表达式为F=mg-mg′．故答案为：mg-mg′．
点评：解决实验的根本是明确实验原理，然后熟练应用所学基本运动学规律求解．