问题
计算题
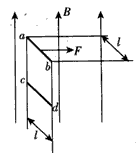
如图所示两根电阻忽略不计的相同金属直角导轨相距为l，它们各有一边在同一水平面内，另一边垂直于水平面，且都是足够长，两金属杆ab，cd与导轨垂直接触形成闭合回路，杆与导轨之间的动摩擦因数均为μ，且最大静摩擦力与滑动摩擦力相等，回路总电阻为R，整个装置处于竖直向上的匀强磁场中。现使杆ab受到F=5.5+1.25 t(N)的水平外力作用，从水平导轨的最左端由静止开始向右做匀加速直线运动，杆cd也同时从静止开始沿竖直导轨向下运动．已知：l=2m，mab=1 kg，mad=0.1 kg，R=0.4 Ω，μ=0.5，g取10 m/s2。求：
(1)磁感应强度B的大小；
(2)cd杆下落过程达最大速度时，ab杆的速度大小。
答案
解：(1)对ab杆：f1=μmabg=5 N
当t=0时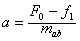
，得a=0.5 m/s2
所以ab杆由静止开始以a=0.5 m/s2的加速度沿导轨匀加速运动
F安=BIl
E=Blv
F安=
根据牛顿第二定律有F-F安-f1=maba
联立以上各式，解得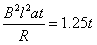
代入数据，解得B=0.5 T
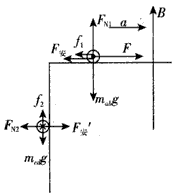
(2)当cd杆下落过程达到最大速度时，cd杆平衡
mabg=f2=μF'安
F'安=BI'L=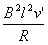
联立以上两式并代入数据，解得v'=0.8m/s