问题
计算题
两根足够长的光滑平行导轨与水平面的夹角θ=30°，宽度L=0.2m，导轨间有与导轨平面垂直的匀强磁场，磁感应强度B=0.5T，如图所示，在导轨间接有R=0.2Ω的电阻，一质量m=0.01kg、电阻不计的导体棒ab，与导轨垂直放置，无初速释放后与导轨保持良好接触并能沿导轨向下滑动。（g取10m/s2）
（1）求ab棒的最大速度。
（2）若将电阻R换成平行板电容器，其他条件不变，试判定棒的运动性质。若电容C=1F，求棒释放后4s 内系统损失的机械能。
答案
解：（1）设某时刻ab的速度为v
则感应电动势E=BLv
电流强度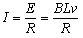
棒所受安培力
则由牛顿第二定律得
，
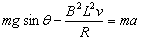
当a=0时，有
（2）设t时刻棒的加速度为a，速度为v，产生的电动势为E，（t+△t）（△t→0）时刻，棒的速度为（v+△v），电动势为E′
则E=BLv，E′=BL（v+△v）
△t内流过棒截面的电荷量
电流强度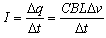
棒受的安培力
由牛顿第二定律，t时刻对棒有
即
故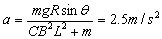
，故棒做匀加速直线运动
当t=4s时，V=at=10m/s，
由能量守恒：