问题
计算题
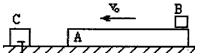
如图所示，长为0.60m的木板A，质量为1kg，板的右端放有物块B，质量为3kg，它们一起在光滑水平面上向左匀速运动，速度
，以后木板A与等高的竖直固定档板C发生碰撞，碰撞时间极短，且碰撞时没有机械能损失，物块B与木板A间的动摩擦因数0.4，取重力加速度
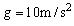，问A、C能否发生第二次碰撞，请通过计算说明理由。若能，则第一次碰撞后再经多长时间A与C发生第二次碰撞；若不能，则第一次碰撞后A做什么运动。
答案
解：由于A与C碰撞没有机械能损失，A碰后原速率弹回，以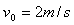
向右运动，若能与C发生第二次撞，则要求A在B对他的摩擦力的作用下，重新向左运动，且B没有滑出A。
设B没滑出A，达到共同速度为v，由动量守恒定律（向左为正），有
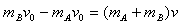
解得
，方向向左
B在A上滑过的距离为SBA，则
解得SBA=0.5m＜L，B不能滑出A，故可以与C发生第二次碰撞。
A与B达到共同速度前做匀变速运动，达到共同速率后做匀速直线运动，设加速度为a
μmBg=mAa， a=12m/s2
A与B达到共同速度经历的时间为t1
t1=v0－v/a=0.25s
此过程A对地向右的位移为s
s= v02－v2/2a=0.125m， t2=s/v=0.125s
所以，第一次碰撞后再与C发生第二次碰撞所经历的时间为：
t=t1+t2=0.375s
