About this time every year, I get very nostalgic(怀旧的). Walking through my neighborhood on a fall afternoon reminds me of a time not too long ago when sounds of children filled the air, children playing games on a hill, and throwing leaves around in the street below. I was one of those children, carefree and happy. I live on a street that is only one block long. I have lived on the same street for sixteen years. I love my street. One side has six houses on it, and the other has only two houses, with a small hill in the middle and a huge cottonwood tree on one end. When I think of home, I think of my street. Only I see it as it was before. Unfortunately things change. One day, not long ago, I looked around and saw how different everything has become. Life on my street will never be the same because neighbors are quickly grown old, friends are growing up and leaving, and the city is planning to destroy my precious hill and sell the property to contractors.
It is hard for me to accept that many of my wonderful neighbors are growing old and won’t be around much longer. I have fond memories of the couple across the street, who sat together on their porch swing almost every evening, the widow next door who yelled at my brother and me for being too loud, and the crazy old man in a black suit who drove an old car. In contrast to those people, the people I see today are very old neighbors who have seen better days. The man in the black suit says he wants to die, and another neighbor just sold his house and moved into a nursing home. The lady who used to yell at us is too tired to bother any more, and the couple across the street rarely go out to their front porch these days. It is difficult to watch these precious people as they near the end of their lives because at once I thought they would live forever.
The “comings and goings” of the younger generation of my street are now mostly “goings” as friends and peers move on. Once upon a time, my life and the lives of my peers revolved around home. The boundary of our world was the gutter at the end of the street. We got pleasure from playing night games or from a breathtaking ride on a tricycle. Things are different now, as my friends become adults and move on. Children who rode tricycles now drive cars. The kids who once played with me now have new interests and values as they go their separate ways. Some have gone away to college like me, a few got married, two went into the army, and one went to prison. Watching all these people grow up and go away makes me long for the good old days.
Perhaps the biggest change on my street is the fact that the city is going to turn my precious hill into several lots for now homes. For sixteen years, the view out of my kitchen window has been a view of that hill. The hill was a fundamental part of my childhood life; it was the hub of social activity for the children of my street. We spent hours there building forts, sledding, and playing tag. The view out of my kitchen window now is very different; it is one of tractors and dump trucks tearing up the hill. When the hill goes, the neighborhood will not be the same. It is a piece of my childhood. It is a visual reminder of being a kid. Without the hill, my street will be just another pea in the pod.
There was a time when my street was my world, and I thought my world would never change. But something happened. People grow up, and people grow old. Places changes, and with the change comes the heartache of knowing I can never go back to the times I loved. In a year or so, I will be gone just like many of my neighbors. I will always look back to my years as a child, but the place I remember will not be the silent street whose peace is interrupted by the sounds of construction. It will be the happy, noisy, somewhat strange, but wonderful street I knew as a child.
小题1:The writer calls up the memory of the street _____________.
A.every year when autumn comes
B.in the afternoon every day
C.every time he walks along his street
D.now that he is an old man小题2:The writer finds it hard to accept the fact that _____________.
A.many of his good neighbors are growing old
B.the lady next door who used to yell at him and his brother is now a widow
C.the life of his neighbors has become very boring
D.the man in his black suit even wanted to end his own life小题3:The writer thinks of the past all the more when he sees those who had grown up with him _____________.
A.continue to consider home to be the center of their lives
B.leave the neighborhood they grew up in
C.still enjoy playing card games in the evenings
D.develop new interests and have new dreams小题4:The biggest change on the writer's street is _____________.
A.removing the hill to make way for residential development
B.the building of new homes behind his kitchen window
C.the fact that there are much fewer people around than in the past
D.the change in his childhood friends' attitude towards their neighborhood小题5:What does the writer mean by saying “my street will be another pea in the pod”?
A.his street will be very noisy and dirty
B.his street will soon be crowded with people
C.his street will have some new attractions
D.his street will be no different from any other street小题6:Which could be a good title for the passage?
A.The Past of My Street will Live Forever
B.Unforgettable People and Things of My Street
C.Memory Street Isn't What It Used to Be
D.The Big Changes of My Street

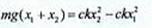
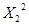 - ck
- ck