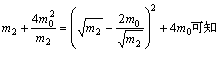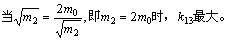问题
计算题
(1)如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为m1的小球从高位h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为m2的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球m2的速度大小v2;
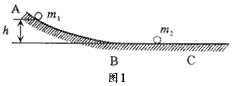
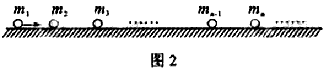
(2)碰撞过程中的能量传递规律在物理学中有着广泛的应用。为了探究这一规律,我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的简化力学模型。如图2所示,在固定光滑水平轨道上,质量分别为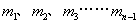 、
、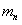 ……的若干个球沿直线静止相间排列,给第1个球初能
……的若干个球沿直线静止相间排列,给第1个球初能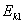 ,从而引起各球的依次碰撞。定义其中第n个球经过依次碰撞后获得的动能
,从而引起各球的依次碰撞。定义其中第n个球经过依次碰撞后获得的动能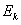 与
与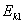 之比为第1个球对第n个球的动能传递系数
之比为第1个球对第n个球的动能传递系数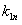 。
。
a.求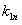 ;
;
b.若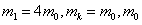 为确定的已知量。求
为确定的已知量。求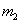 为何值时,
为何值时,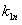 值最大。
值最大。
答案
解:(1)设碰撞前的速度为v10,根据机械能守恒定律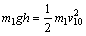 ①
①
设碰撞后m1与m2的速度分别为v1和v2,根据动量守恒定律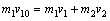 ②
②
由于碰撞过程中无机械能损失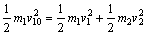 ③
③
②、③式联立解得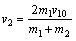 ④
④
将①代入④得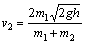
(2)a.由④式,考虑到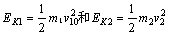
得根据动能传递系数的定义,对于1、2两球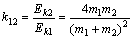 ⑤
⑤
同理可得,球m2和球m3碰撞后,动能传递系数k13应为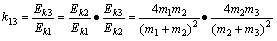 ⑥
⑥
依次类推,动能传递系数k1n应为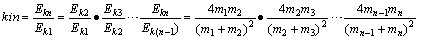
解得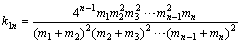
b.将m1=4m0,m3=m0代入⑥式可得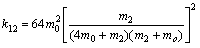
为使k13最大,只需使
由