问题
计算题
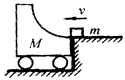
在光滑水平地面上放有一质量为M带光滑弧形槽的小车，一个质量为m的小铁块以速度v沿水平槽口滑去，如图所示，求：
（1）铁块能滑至弧形槽内的最大高度H；（设m不会从左端滑离M）
（2）小车的最大速度是多大？
（3）若M=m，则铁块从右端脱离小车后将作什么运动？
答案
解：（1）当铁块滑至弧形槽中的最高处时，m与M有共同的水平速度，等效于完全非弹性碰撞，由于无摩擦力做功，则系统减小的动能转化为m的势能
根据系统水平动量守恒：mv=(M+m)v′
而mgH=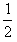
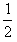mv2－(m+M)v′2
可解得Hm=Mv2/［2g(M+m)］
（2）当铁块滑至最大高度后返回时，M仍在作加速运动，其最大速度是在铁块从右端脱离小车时，而铁和小车间挤压、分离过程，属于弹性碰撞模型，有：
mv=mvm+MVM
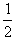mv2=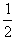
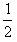mv2m+
Mv2M
联立得vm=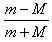
v，vM=
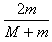v
所以，小车的最大速度为2mv/(M+m)
（3）当M=m时，v′m=0，vM=v，铁块将作自由落体运动